In the "All Lean Books And Where To Find Them" article, I advise a number of formalization books (Formalizing Mathematics => Theorem Proving in Lean => Mathematics in Lean) to people who want to learn to formalize mathematics in Lean.
This was based off the contents and relative difficulty of the books. Now, after I participated in the formalization of the Carleson's theorem, my mind has changed on this a bit. I think there is little sense in reading Lean textbooks about formalization1 - the easiest route to learning formalization is to:
get the hang of the logic behind how goals and hypotheses interact in Lean (play the Natural Language Game)
learn ~10 basic tactics in Lean (do a couple of chapters in Formalizing Mathematics)
dive into a real formalization project (ongoing formalization projects can be found on Lean zulip).
There is one caveat, however, one more skill that needs to be learned - one needs to know how to search for theorems in Lean 4. As Will Crichton mentions in his "How to Make Mathematicians Into Programmers" talk, theorem search is essential for formalization, and yet it is not taught in any Lean textbook.
This is my attempt at explaining how to search for theorems in Lean 4.
___ 1 I think reading books about formalization might be most useful after you acquire the motor skill of formalizing real things in a real project
Overview
In Lean, there are two main types of search engines:
"neural/vector-based" search engines (Moogle, LeanSearch, Search-Mathlib) Neural search engines work via LLM embeddings, and return approximate matches. Neural search engines can be used when you're not yet sure what's likely to be present in Mathlib, or when you're not in the mood for typing out a proper formal search string, and prefer to quickly query something in natural language.
"formal" search engines (Loogle, Mathlib's exact?) Formal search engines work via Lean metaprogramming, and return all theorems in Mathlib that match your query. Formal search engines are predictable and comprehensive, but do require you to have a good idea on the shape of the statement of the searched-for theorem, and do require you to be careful with the symbols you use.
Throughout this post, we'll be searching for the theorem Metric.ball_subset_ball from Mathlib, a theorem telling us that if two balls share a center, then the ball with a smaller radius is a subset of the ball with a bigger radius:
theorem Metric.ball_subset_ball {α : Type u} [PseudoMetricSpace α] {x : α} {ε₁ : ℝ} {ε₂ : ℝ}
(h : ε₁ ≤ ε₂) : Metric.ball x ε₁ ⊆ Metric.ball x ε₂
Neural search engines will be queried with from: x ≤ y, to: ball c x ⊆ ball c y, formal search engines will be queried with Metric.ball ?c ?_ ⊆ Metric.ball ?c _.
NEURAL SEARCH
Moogle, LeanSearch and Search-Mathlib are vector-based search engines.
They all share a similar technical underpinning - per each theorem in Mathlib, they take a formal statement of that theorem, create the semantic embedding from it, and put it into the vector database. One vector == one theorem; theorems are considered similar when the cosine distance between their corresponding vectors is small.
When searching for theorems using a neural search engine, the user can type anything they like - LaTeX formulas, approximate theorem names, proof term descriptions, natural language sentences - semantic search can digest all of it. Any such user query will be converted into an embedding vector of its own.
So - we input any kind of a query string, this query string is converted into a vector of its own, and, using cosine similarity, we find the theorem vectors that are most similar to our query vector. Those are our search results.
There is an interesting question of how exactly one should best query semantic search engines.
Anecdotally, if you input something obviously silly, like theorem name that has many letters "z", semantic search will happily return theorem List.zip_unzip. If you input theorem that they learn in school, semantic search will happily return theorem Nat.sq_sub_sq (a : ℕ) (b : ℕ) : a ^ 2 - b ^ 2 = (a + b) * (a - b).
LeanSearch paper (link) offers the following categorization of all search queries:
natural-descripton "If there exist injective maps of sets from A to B and from B to A, then there exists a bijective map between A and B."
LaTeX-formula "If there exist f: A → B injective, g: B → A injective, then there exists h: A → B bijective."
In my experience, theorem-name queries are exceedingly rare, most lemmas you might want to find do not have names. Similarly, I never had the need to query a LaTeX-formula. Technically, we do have some LaTeX in our formalization blueprints - however blueprints are not that detailed, practically all theorems we will need during the formalization process are glossed over in a blueprint.
So, what gets used in practice is natural-descriptons and Lean-terms. In fact, what I find most useful is a heavy mix of these two. For example, LeanSeachClient (a Lean library that lets you interact with Moogle and LeanSearch via a Lean command) offers the following example of a query: "If a natural number n is less than m, then the successor of n is less than the successor of m", which would get classified as a purely natural-language query. And here is the query I would use instead: "natural numbers. from: n < m, to: n + 1 < m + 1", which belongs to a mix of natural-descripton and Lean-term categories.
No matter what query category you decide to go for, during the formalization process you have to perform the same ritual:
DISTILL THE ESSENCE OF YOUR SITUATION What usually happens is you have a hypothesis with type d ^ m < d ^ n * d * 25 - d ^ n * 4, and you want to turn it into a hypothesis with type d ^ m < d ^ (1 + n) * 25 - d ^ n * 4. You can try to query the following string from: d ^ m < d ^ n * d * 25 - d ^ n * 4 to: d ^ m < d ^ (1 + n) * 25 - d ^ n * 4, however it won't find anything of use. You need to distill your situation to its bare essence! So, you manually turn your initial query into the following query: from: (a ^ b) * a to: a ^ (b + 1)
SEARCH You submit the distilled search query to the vector search engine. It returns a number of theorems to you. You decide which theorem looks good based on its signature. You copypaste it into your editor.
TYPE PUZZLE Now comes the puzzle game where you try to fit your existing hypotheses into this theorem's signature. This usually involves dealing with coercions (e.g., turning your Nats into Reals), dealing with associativity/commutativity, providing additional data to the tactic (e.g., positivity of some variable), and, finally, matching hypotheses to arguments.
Now - even though semantic search engines all share the same technical underpinning, there is some variation in what exactly they convert into the embedding vector, in how frequently they sync with the latest Mathlib, etc. Below I describe the main search engines present in Lean 4 at the moment, how they differ, and my personal experience with them.
Moogle is a search engine by Morph Labs, and, to my knowledge, Moogle was the first semantic search engine for proof assistants ever created - or, at the very least, the first semantic search engine actively used by the community. After Moogle, other such efforts followed - a competing search engine for Lean 4 (LeanSearch) and a search engine for Coq (ProofDB).
At the very least from November 2023 to July 2024, Moogle was the leading semantic search engine for Lean. Anecdotally - July 24th 2024 Kevin Buzzard was giving the "The state of the art in the formalization of research-level mathematics" talk during the "Interactive Theorem Proving in Education and Research" workshop (link). During the questions section, I asked "what do people use to search for theorems in Lean lately - Loogle, Moogle, ReProver, #find tactic, something else completely?". To which Kevin responded with something along the lines of "Moogle! Once there was a 6-hour Moogle outage, and that was the only thing zulip discussed".
Despite the fact that Moogle was a pioneer in this space, at the moment Morph Labs doesn't seem interested in keeping Moogle up to date with the current Mathlib, or in improving the tech behind it, or in open-sourcing the codebase.
Moogle held the leadership among semantic search engines for a few months, but I get a feeling LeanSearch is at least on par with Moogle nowadays.
MY USE I have a preference for LeanSearch at the moment. This preference is not based on any proper statistical comparison, it's based on the intuitive "hey, LeanSearch returns the desired theorem on 3rd place, and Moogle returns it on 10th place", repeated a few times during my formalization experience. Moogle is functional too, however, and is worth trying out - maybe you'll have better luck with your queries.
LeanSearch is the semantic search engine I use the most. Generally, LeanSearch just has a higher chance of returning what I'm searching for, on higher positions than Moogle would have it.
Moogle neither open-sourced their implementation nor wrote a paper about it, but, from what I understand, what they are doing internally is they turn [Lean statement] into the embedding vector and that's it. LeanSearch published a paper, so we know it takes [Lean statement, docstring, related defitions, natural language version of this theorem generated using GPT-3], and turns that into the embedding vector.
It's unclear whether that is the main reason behind LeanSearch showing a better performance - there is also a question of whether the theorem is present in the search engine at all. There were cases when I couldn't find a theorem in Moogle via the search query that's a direct copypaste of that theorem's name - it's possible that Moogle simply doesn't refresh their database frequently enough to keep up to date with the latest Mathlib. On the other hand, I just tried to recreate that situation, and what I found instead is the opposite - on March 1st 2025, Real.rpow_le_rpow_of_exponent_le (a theorem that does exist in current Mathlib) is returned by Moogle and not returned by LeanSearch!
In either case - both in terms of the presence of theorems, and in terms of the engine's ability to return the desired theorem as one of the first results, LeanSearch has generally been more consistent for me.
As you can see in the screenshot, LeanSearch has one unusual feature - the "Query Augmentation" button. What it does is it turns your query string into a natural language description using GPT-4. For example, it turns our "from: x ≤ y, to: ball c x ⊆ ball c y" query into "Monotonicity of Balls with Respect to Radius: In a metric space, if the radius of a ball centered at a point c is increased from a value x to a value y, where x is less than or equal to y, then the ball with radius x is entirely contained within the ball with radius y. This means that every point within the smaller ball is also within the larger ball" query. I do use that on occasion, but regular search normally suffices.
Published, quite unfortunately, on the same day as LeanSearch - this is a simple model on huggingface. Returns pretty good results, but this was merely a training exercise for the author as he states in his introduction on zulip.
I think the zulip message by Deming Xu is worth a read - with only 100 lines of Lean code (adjusted code taken from another library) + 200 lines of Python code (100 of which is just setting up the web page), he managed to create a search engine that performs reasonably well, which is quite inspiring to anyone who wants to experiment with semantic search in Lean 4.
The principles are similar to what LeanSearch and Moogle are doing - convert all theorems into vectors, convert a search query into a vector, put all of these vectors into vector database, and determine the theorem vectors closest to the search query vector. Deming turns [theorem name, theorem statement, theorem docstring] into a vector.
MY USE I don't use it (and it was never intended for use!), as there exist LeanSearch and Moogle.
FORMAL SEARCH
As described above, formal search is search that's performed via Lean's metaprogramming - consider it a function written in Lean that compares all existing theorem signatures to the precise search string you provide.
Loogle is a search tool by Joachim Breitner. Loogle descended from Mathlib's #find (Joachim tried to merge two #find PRs, #6643 and #6363, into Mathlib, but the reviews went on for too long, so he just went ahead and created github.com/nomeata/loogle and loogle.lean-lang.org); and was reportedly inspired by Haskell's Hoogle (link). Even though Loogle was initially a wrapper around #find, Joachim says Loogle and #find significantly diverged in both functionality and implementation by now.
When searching for theorems in Loogle, you should: 1) think of what the theorem signature is likely to be 2) liberally use ?_ (hole) and ?anyString (named hole) for the subexpressions that you cannot predict the exact structure of.
Generally, it feels similar to how you'd be searching for a theorem with a regex. The key is to keep the query as general as possible, while still narrowing down the results to a shortish list. So, don’t search for: Real.cos _ * Real.cos _ + Real.sin _ * Real.sin _ = 1 - who knows if the lemma has these terms in that exact order, or if the lemma is maybe using Real.cos _ ^ 2! A better search query might be Real.cos, Real.sin (i.e., just list the constants you expect to appear anywhere in the statement). Do not use a rigid expression pattern if you don’t have to.
One curious fact about the #find command is it doesn't return theorems defined in your local environment. It's understandable why Moogle and LeanSearch don't return local results, that would require parsing the project (though it's not expensive, I do think semantic search engines will implement a "submit a project to parse" functionality at some point), but formal search should be able to do it with little programming overhead, for example exact? tactic does return local lemmas. From what I understand, this happens because #find uses DeclCache, which gives the command a fast startup time, but precludes access to the local lemmas (link). In either case - you will probably want to use Loogle instead of #find, and Loogle only has access to Mathlib. The recently added to Mathlib #loogle command calls the loogle.lean-lang.org api rather than executing Loogle source code from within your project, so that command also only has access to Mathlib. As I will mention later in the article, the easy way to have a per-project Loogle-like functionality is to literally CMD+F, so it's understandable why making Loogle work locally is not a priority.
MY USE I use Loogle as frequently as I use LeanSearch! I think a good rule of thumb is: when you're new to formalization, you should start by using LeanSearch (because you don't yet have a gut feeling for "what kind of theorem is likely to exist in Mathlib"), and then add Loogle to your toolbox.
I mostly use Loogle from within vscode (this functionality is provided by the default vscode-lean extension), this is what it looks like:
Mathlib's exact? (previously library_search)
At some point, we used to have a tactic called library_search - later on, it forked into rw?, apply?, and exact?. All of these tactics only work on the current goal, in particular:
rw? will find all rewrites that we can do on a goal.
apply? will find all theorems that are legal to execute on a goal.
exact? will find all theorems that are legal to execute on a goal, AND that do close the goal.
This might be my lack of imagination, but I'm yet to find a use case for rw? or apply?. exact?, on the other hand, might be my most frequently used search method of all.
The general workflow with exact? is as follows:
Look at your proof state, and come up with the next desired hypothesis. For example, suppose you want a hypothesis h: x^3 ≤ x^5.
Write have h : x^3 ≤ x^5 := by exact?.
Enjoy your result - exact? will gift you a have h : x^3 ≤ x^5 := by exact pow_le_pow_right₀ h1 h2.
Similarly, you can come up with the next desired goal, and use suffices to make exact? search for it. For example, if your next desired goal is 2 + 2 = 4, you can write suffices 2 + 2 = 4 by exact?.
As wonderful as exact? is, it's a very straightforward tool - it won't do anything fancier than a 1-step theorem application. This has a few consequences. First of all, exact? won't find anything if any of the necessary hypotheses are lacking. So, if you know that your goal will require a particular hypothesis that is not yet in context, do define that hypothesis before calling exact?. For example, if you want to call have h : x/x = 1 := by exact?, you must explicitly define have h : x ≠ 0 := by positivity in your context. Secondly, exact? won't deal with casting, make sure all of your hypothesis and the goal are cast appropriately before calling exact?. Moreover, exact? won't deal with associativity and commutativity, the hypothesis you're searching for must really be one-step away from your current context.
The key to using exact? is the gradual acquisition of the intuition for what theorems are likely to be present in Mathlib, and thus a skillful creation of the "desired hypothesis type" that really is one step away from your current context, and therefore will be easily deduced by exact?.
Unlike all the search tools mentioned previously, exact? does search among the locally available lemmas. More precisely, exact? can access:
all the lemmas in the current file defined BEFORE the exact? call
all lemmas from Lean.Init
all lemmas from the imported hierarchy tree (so, all lemmas from the imported modules, AND from the modules those modules imported, AND from the modules...)
MY USE I use exact? all the time, and I do not use apply? and rw? at all.
OTHER
LeanCopilot, LeanStateSearch
LeanCopilot's select_premises tactic returns "theorems relevant to the current state of the proof" (as customary in machine learning, when they say "premises" - they mean "theorems").
With LeanStateSearch, you can use #statesearch command after importing Mathlib.
From my understanding, these tools have a similar technical underpinning - or, at the very least, they take the same information in (current state of the proof) and give the same information out (the names of the relevant theorems). I'm yet to try out either of them in my day-to-day formalization workflow, but below you can see what my first attempt at using #statesearch was like. You can see that it did find a relevant theorem, so it can work - at the very least for one of the last steps of your proof.
Powerful tactics
Something not immediately obvious is that powerhouse tactics such as linarith/omega/ring/simp/simp_all/aesop are also, practically, search. With those tactics, the idea is that you see what your goal is like, and you have a hunch for whether one of these tactics would solve it. For example, if you have a set of linear inequalities, and you want to prove a linear inequality, and all of these inequalities are simple, then linarith should succeed. If not, try to make the inequalities in question even more simple, and repeat the linarith attempt. Right now I'm going by such hunches, but I do kind of wish there was a flowchart for when exactly to try each such tactic, and what other such tactics are available.
CMD+F
CMD+F in your editor is also search, don't neglect it! In fact it's frequently the best way to find theorems defined in your Lean project. The Carleson project is a few-dozen-files project, and CMD+F-ing for a specific constant tends to return 3-10 entries - it's typically reasonably easy to read through them all!
LLMs
Usage of LLMs is also search. As described above, none of the semantic search engines allow per-project search. The only way to get an idea for whether some theorem exists in Carleson is literally looking through the project files, one by one; and maybe CMD+F-ing for certain symbols.
So, when I need to find a theorem in my local project, I use the paid version of Claude to create a quick ad-hoc semantic search engine by copypasting the relevant Carleson files into Claude's project knowledge, like this:
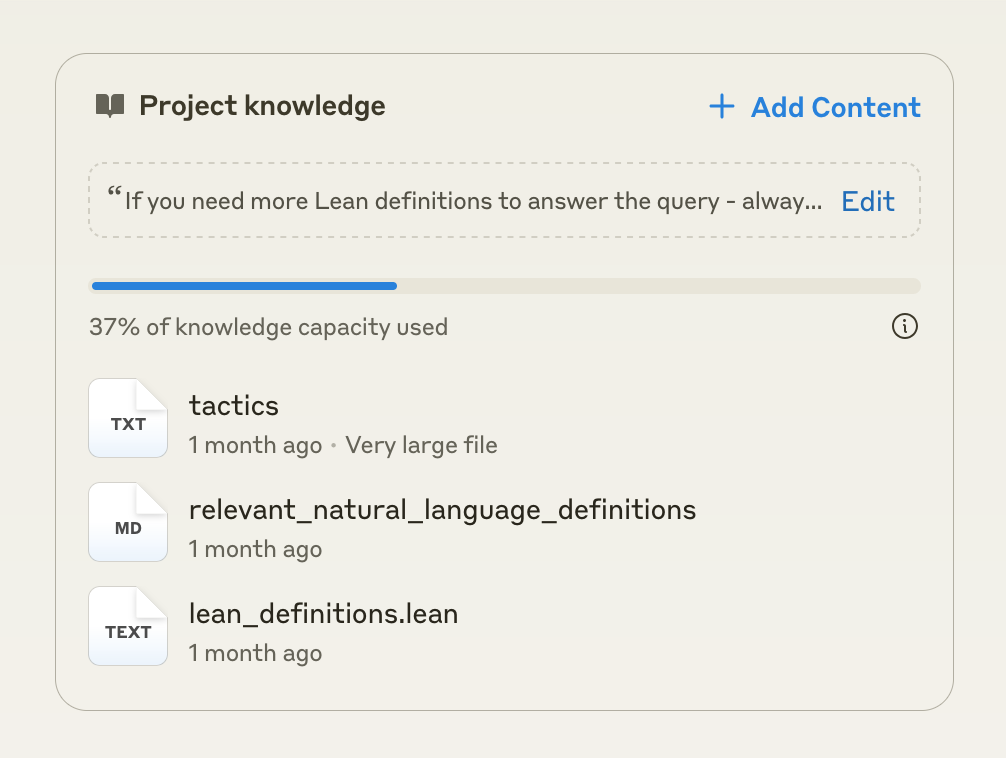
Which I then query like this:
Copypasting entire .lean files is wasteful of course, we don't need the bodies of the proofs, we only need the statemets. A quick way to solve that would be to install LeanDojo or LeanTrainingData, get the statements of all theorems in Carleson's, and feed that to Claude as a single file.
