Metaprogramming in Lean

A post giving an overview of metaprogramming in Lean. There is of course a book on Metaprogramming in Lean, consider this an introductory chapter that I felt I lacked. 

UPDATE: this is now an "Overview" chapter in Metaprogramming in Lean, go read it directly in the book, the text is more thought-through there & the images are prettier their (see, here you get typos!).

If you have done some metaprogramming in languages such as Ruby, Python or Javascript, it probably took a form of making use of predefined metaprogramming methods in order to define something on the fly. For example, in Ruby you can use Class.new and define_method to define a new class and its new method (with new code inside!) on the fly, as your program is executing.

We don't usually need to define new commands or tactics "on the fly" in Lean, but spiritually similar feats are possible with Lean metaprogramming, and are equally straightforward, e.g. you can define a new Lean command using a simple one-liner elab "#help" : command => do ...normal Lean code....

In Lean, however, we will frequently want to directly manipulate Lean's CST (Concrete Syntax Tree, Lean's Syntax type) and Lean's AST (Abstract Syntax Tree, Lean's Expr type) instead of using "normal Lean code", especially when we're writing tactics. So Lean metaprogramming is more challenging to master - a large chunk of the "Metaprogramming in Lean" book is contributed to studying these types and how we can manipulate them.

Connection to compilers

Metaprogramming in Lean is deeply connected to the compilation steps - parsing, syntactic analysis, transformation, and code generation.

Lean 4 is a reimplementation of the Lean theorem prover in Lean itself. The new compiler produces C code, and users can now implement efficient proof automation in Lean, compile it into efficient C code, and load it as a plugin. In Lean 4, users can access all internal data structures used to implement Lean by merely importing the Lean package.

Leonardo de Moura, Sebastian Ullrich (paper)

The entirety of metaprogramming in Lean can be captured in 3 steps - parsing, elaboration, and evaluation. The compiler sees a string of Lean code, say "let a := 2", and the following process unfolds:

1. apply a relevant syntax rule ("let a := 2" ➤ Syntax)
   During the parsing step, Lean applies all declared syntax rules to turn a string of Lean code into the Syntax object. syntax rules are basically glorified regular expressions - when you write a Lean string that matches a certain syntax rule's regex, that rule will be used to handle subsequent steps.
2. apply all macros in a loop (Syntax ➤ Syntax)
   Each macro simply turns the existing Syntax object into some new Syntax object. Then, the new Syntax is processed in a similar way (steps 1 and 2), until there are no more macros to apply.
3. apply a single elab (Syntax ➤ Expr)
   Finally, it's time to infuse your syntax with meaning - Lean finds an elab method that's matched to the appropriate syntax rule by the name argument (both the syntax rule and elab method have this argument, and they must match). The newfound elab returns some Expr object.

Expression (Expr) is then converted to the executable code during the evaluation step - we don't have to specify that in any way, the Lean compiler will handle that for us.

Manual conversions between Syntax/Expr/executable-code

Lean will execute the afforementioned parsing/elaboration/evaluation steps for you automatically if you use syntax, macro and elab commands, however, when you're writing your tactics, you will also frequently need to perform these transitions manually. You can use the following functions for that:

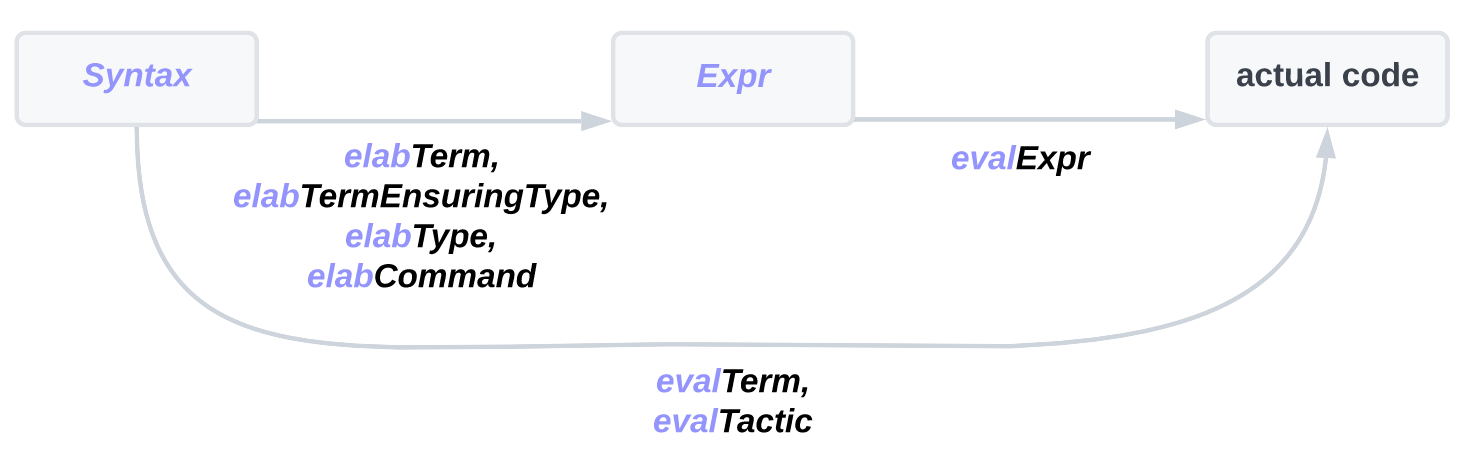
Note how all functions that let us turn Syntax into Expr start with "elab", short for "elaboration". Elaboration is a loaded term in Lean, for example you can meet the following usage of the word "elaboration", which defines elaboration as "taking a partially-specified expression and inferring what is left implicit":

When you enter an expression like λ x y z, f (x + y) z for Lean to process, you are leaving information implicit. For example, the types of x, y, and z have to be inferred from the context, the notation + may be overloaded, and there may be implicit arguments to f that need to be filled in as well.

The process of taking a partially-specified expression and inferring what is left implicit is known as elaboration. Lean's elaboration algorithm is powerful, but at the same time, subtle and complex. Working in a system of dependent type theory requires knowing what sorts of information the elaborator can reliably infer, as well as knowing how to respond to error messages that are raised when the elaborator fails. To that end, it is helpful to have a general idea of how Lean's elaborator works.

When Lean is parsing an expression, it first enters a preprocessing phase. First, Lean inserts "holes" for implicit arguments. If term t has type Π {x : A}, P x, then t is replaced by @t _ everywhere. Then, the holes — either the ones inserted in the previous step or the ones explicitly written by the user — in a term are instantiated by metavariables ?M1, ?M2, ?M3, .... Each overloaded notation is associated with a list of choices, that is, the possible interpretations. Similarly, Lean tries to detect the points where a coercion may need to be inserted in an application s t, to make the inferred type of t match the argument type of s. These become choice points too. If one possible outcome of the elaboration procedure is that no coercion is needed, then one of the choices on the list is the identity.

(Theorem Proving in Lean 2)

These definitions are not mutually exclusive - elaboration is the transformation of Syntax into Exprs - it's just so that for this transformation to happen we need a lot of trickery - we need to infer implicit arguments, instantiate metavariables, perform unification, resolve identifiers, etc. etc. - and these actions can be referred to as "elaboration" on their own; similarly to how "checking if you turned off the lights in your apartment" (metavariable instantiation) can be referred to as "going to school" (elaboration).

3 essential functions and their syntax sugars

Now, when you're reading Lean source code, you will see 11(+?) commands specifying the parsing/elaboration/evaluation process.  Most of them are syntax sugar, and you only need 3 commands to do metaprogramming in Lean:

• syntax rule: syntax (name := xxx) ... : command
  
  For example, syntax (name := xxx) "#help" "option" (ident)? : command is a syntax rule that will match (remember the regex analogy) all strings in the form of "#help option hi.hello" or just "#help option". 
  Other widespread syntax categories are tactic and term, all of these are used in different physical places in your code.
   
• macro: @[macro xxx] def ourMacro : Macro := ...
  
  For example, @[macro xxx] def ourMacro : Macro := λ stx => match stx with | _ => `(tactic| pick_goal 2). Whenever your Lean code matches the syntax rule with the name xxx, this macro will be applied.
  If the syntax rule was syntax (name := xxx) "swap" : tactic, this macro will syntactically turn swap into pick_goal 2 - and the subsequent elaboration step will be handled by the pick_goal 2 syntax rule.
   
• elab: @[command_elab xxx] def ourElab : CommandElab := ...
  
  For example, @[term_elab our_help] def ourElab : TermElab := λ stx tp => (Expr.app (Expr.const `Nat.add [])).
  Now, TermElab stands for Syntax → Option Expr → TermElabM Expr, so the elaboration function is expected to return the Expr object.
  There also exists CommandElab, which stands for Syntax → CommandElabM Unit, so it shouldn't return anything.
  Tactic stands for Syntax → TacticM Unit, so it shouldn't return anything either.
  This corresponds to out intuitive understanding of terms, commands and tactics in Lean - terms return a particular value upon execution, commands modify the environment or print something out, and tactics modify the proof state.
   

These syntax (name := xxx) ... : command, @[macro xxx] def ourMacro : Macro := ... and @[command_elab xxx] def ourElab : CommandElab := ... are the 3 essential, low-level functions, and you can get away with them only. Lean standard library and Mathlib use many syntax sugars, however, so it's well worth the effort to memorize these. I'm summing them up in the next diagram.

Order of execution: syntax, macro, elab

I have hinted at the flow of execution of these three essential functions here and there, however here I want to lay it out explicitly. The order of execution follows the following pseudocodey template: (syntax; macro)+ elab.

Consider the following example.

The process is as follows:

match appropriate syntax rule (happens to have name := xxx) ➤
apply @[macro xxx] ➤

match appropriate syntax rule (happens to have name := yyy) ➤
apply @[macro yyy] ➤

match appropriate syntax rule (happens to have name := zzz) ➤
can't find any macros with name zzz to apply, 
so apply @[command_elab zzz].  🎉.

The behaviour of syntax sugars (elab, macro) can be understood from these first principles.

Assigning meaning: macro VS elaboration?

In principle, you can do with a macro (almost?) anything you can do with the elab function. Just write what you would have in the body of your elab as a syntax within macro. However, the rule of thumb here is to only use macros when the conversion is simple and truly feels elementary to the point of aliasing. Here are some related discussions from Lean Zulip.

I'm wondering where people think the border between "use a macro" and "use an elaborator" for this actually is. In my mind this has so far been that as soon as types or control flow is involved a macro is probably not reasonable anymore.

Henrik Böving (zulip thread)

I also agree (this was also discussed in another thread) that using Syntax for logic and control is far from ideal, and it is best to work at the Meta/TermElab level for this. Lean 4 macros are superb for notation and for creating some shortcuts. But passing around bits of syntax as proxies for function arguments is very fiddly.

Understanding Syntax is very much necessary. I think the point both Jannis Limperg and I are making is that one should avoid readers driven to using macros and working with syntax where it is better to use Meta/Elab and work with expressions, simply because one can start working with macros a bit quicker.

Siddhartha Gadgil (zulip thread)